Here I propose an extension of the standard NEAT search technique with the intention of refining NEAT's ability to search the Neural Network topology space. The overall concept is a simple one; the original implementation of NEAT by Kenneth Stanley searches topologies by increasing complexity by way of additive mutations that add new connections and neurons. Others[1] have shown that NEAT's ability to find solutions can be improved by using subtractive mutations concurrently with the normal additive mutations. Here I describe a variation whereby the NEAT search switches between pure complexifying (additive) and pure simplifying (subtractive) phases. It is suggested that this technique better preserves NEAT's ability to search complex topologies but also allows the search to periodically prune away redundant structures. This pruning has the benefit of allowing NEAT to explore a wider range of simple topologies and also speeds up the speed of a search by lowering the overall complexity of the genome population.
Genome bloat can be described as the accumulation of redundant genes within a population, resulting in longer and longer genomes with no associated improvement in fitness. Longer genomes take up more computer memory, take longer to manipulate in crossover, mutation etc. algorithms and describe larger networks, which in turn take longer to simulate. One major detrimental effect of bloat then is a slow down in the overall speed of a search.
Original NEAT's primary means of searching topology is via complexification - adding new neurons and connections - there are no deletion mutations in the original NEAT implementation or indeed in past versions of SharpNEAT. This has often led to discussions on the NEAT yahoo group about whether NEAT is susceptible to genome bloat. Before I progress I will attempt to summarize the points raised in the yahoo group discussions here.
Firstly there has been some disagreement on what actually constitutes bloat. Above I described it as redundant genes, but how do we distinguish between a useful gene and a redundant one? One way is to examine the sub-structures within a network that genes describe. It is a simple task to systematically test networks with various sub-structures removed, if a structure's removal causes a network's fitness to drop then it is useful, otherwise it is functionally redundant*. However, functionally redundant structure is not necessarily redundant to the NEAT search as a whole, some of these structures may get connected to in future additive mutations in a way that integrates them into beneficial structures. These then can be thought of as speculative structures. NEAT needs to keep a healthy number of speculative structures within a population in order to work, in fact this is at the heart of how NEAT works and without them NEAT would be a very limited technique.
Consider what would happen if we ensured that functionally redundant structures were kept out of a population altogether - the bulk of additive mutations would be discarded, only mutations that were immediately beneficial would be kept. Quite often though, no single addition can improve a network's fitness, often the accumulation of several additions is required to form a structure that is beneficial. In order for NEAT to find these structures it must keep some functionally redundant, speculative structure in it's population at all times. With this in mind we can see that bloat and speculative structure are two intimately related concepts.
It turns out that the use of speciation within NEAT applies downward pressure on the amount of speculative structure in a population. This is because each species is tracked. When a species reaches a certain number of generations(the 'drop-off' age) without improving, it is culled from the population along with all of its speculative structures, giving other species a larger 'slice' of the population 'pie'. Meanwhile, if simple species are doing well then they will be kept in the population, and any offspring they generate that are more complex by way of additive mutations will form new species, thus preserving simple species - as long as they are doing well.
There is a problem though, speciation's ability to apply downward pressure on speculative structure is very limited when a search reaches a fitness plateau. If no improvements are being found in a population then each species will be culled one by one as they reach the drop-off age, and in turn newer more complex species will fill the void, the complexity of population then escalates quickly.
Another problem is that of 'piggy back' structure. As an example consider that a search has complexified and it has paid off by resulting in a good genome, that genome now takes up a larger portion of the population (through fitness sharing) and itself probably starts to spawn new species. Unfortunately, because original NEAT has no deletion mutations, any speculative structure that didn't actually contribute to the increased fitness is still maintained and will also make it to any spawned species. This accumulation of speculative structure could also result in the complexity of the population increasing.
We have established that some speculative structure is required for searches to progress, but how much? Original NEAT applies some downward pressure on a population's complexity by speciation, but when a fitness plateau is reached that downward pressure is lessened or completely lost and complexity rises unhindered. It has been suggested that this rise in complexity is a positive thing, because if a fitness plateau has been reached then that can be taken as an indication that other areas of the search space need to be explored, and complexification does indeed move a search into new areas of the search space. However, I have two points to make here:
1) Complexification moves us into a more complex and speculative search space that is far less likely to find good solutions, so we should ensure we have exhausted the lower dimensional space of simple topologies before complexifying. Original NEAT's propensity to complexify its way out of a fitness plateau will often prevent a proper exhaustive (or at least more thorough) search of simple topologies. This can be partly alleviated by using a larger genome population, but there is a relatively low practical limit to the size of population that can be supported in SharpNEAT and other NEAT implementations, due to memory and speed limitations.
2) Complexifying places a search into a higher dimension search space, and as the dimensionality rises the chances of finding a good structure lessen and quickly become infinitesimal. Therefore I theorize that complexifying out of a fitness plateau is only appropriate for short periods, and that once complexity has risen by some fixed amount without an associated rise in fitness, then the search is unlikely to progress. Experimentation with SharpNEAT backs up this idea. One exception to this rule is that a small, simple sub-structure may still be found in the higher dimensional space, but the likelihood of this is also severely diminished because the search speed slows significantly as population complexity rises. Therefore although simple sub-structures can be found in relatively complex genomes, this is an inefficient way of finding such structures.
Ideally then we would like to limit the rate at which NEAT complexifies so that we can more thoroughly search simple topologies before moving on to more complex ones. One approach might be to simply reduce the 'add neuron' and 'add connection' mutation rates, this does reduce the rate of complexification but only serves to better search the connection weight space of the limited set of topologies that are in a population at a given time, it does not help search a wider range of simple topologies.
Another approach that might be taken to ensure the space of simple topologies is more thoroughly searched is that of blended searching. Blending refers to the use of a mixture(or blend) of additive and subtractive mutations and in fact this approach has been shown to have some benefit[1]. Subtractive mutations help keep the complexity of a population down, however, in a blended search experiment described later the downward pressure on complexity exerted by subtractive mutations was found to be very light. The likely reason is that structures deleted in one genome are still present in other genomes, and will therefore be re-propagated through a population via crossover as fast as they are removed by subtractive mutations.
Also note that in a blended search new and old structures have an equal chance of being deleted, and that a possible detrimental effect of this is that new structures may not be given a reasonable amount of time to be properly evaluated.
As an alternative to blended searching I propose the use of 'phased' searching, so called because the NEAT search switches between a complexifying phase and a simplifying(or pruning) phase.
Phased searching works as follows:
1) Before the search starts proper, calculate a threshold at which the prune phase will begin. This threshold is the current mean population complexity (MPC)** plus a specified pruning phase threshold value which typically might be between 30-100 depending on the type of experiment.
2) The search begins in complexifying mode and continues as traditional NEAT until the prune phase threshold is reached.
3) The search now enters a prune phase. The prune phase is almost algorithmically identical to the complexifying phase, and the normal process of selecting genomes for reproduction, generating offspring, monitoring species compatibility, etc. all takes place. The difference is that the additive mutations are disabled and subtractive ones enabled in their place. In addition only asexual reproduction (with mutation) is allowed. Crossover is disabled because this can allow genes to propagate through a population, thus increasing complexity.
4) During each generation of the pruning phase a reading of the MPC is taken, this will normally be seen to fall as functionally redundant structures are removed from the population. As pruning progresses the MPC will eventually reach a floor level when no more redundant structure remains in the population to be removed. Therefore once MPC has not fallen for some number of generations (this is configurable, between 10-50 works well), we can reset the next pruning phase's threshold to be the current MPC floor level + the pruning phase threshold parameter and switch into a complexifying phase. The whole process then begins again at (2).
One small modification was made to the above process, and that is to not enter prune phase unless the population fitness has not risen for some specified number of generations. Therefore if the complexity has risen past the pruning phase threshold but the population fitness is still rising then we hold off the pruning phase until the fitness stops rising.
A phased search has a number of benefits:
1) The complexifying phase operates exactly the same as traditional NEAT and is able to speculatively complexify to find solutions in a higher-dimension search space. It does not suffer from the premature loss of structures that blended searching does - although note that this has not yet been shown to be detrimental.
2) The pruning phase removes all or most of the functionally redundant structure in a population, moving the search back to a baseline lower-dimensional search space that is faster to search.
3) Each pruning phase threshold is set relative to the previous pruning phase's complexity baseline. This keeps the complexity of the population between the baseline of pure functional structure and a threshold of some specified level above the baseline. Although this does cause the complexity to oscillate or zig-zag up and down, it does have the desired effect of keeping a small proportion of speculative structure in the population most of the time, whilst preventing complexity from rising beyond useful levels. Also not e that the baseline level of complexity will rise throughout a search, as new beneficial structures are discovered.
The actual pruning technique used in the pruning phase is simple but requires some explanation. To support pruning, two new types of genome mutation have been added to SharpNEAT, these are connection deletion and neuron deletion. Connection deletion is very simply the deletion of a randomly selected connection, all connections are considered to be available for deletion. When a connection is deleted the neurons that were at each end of the connection are tested to check if they are no longer connected to by other connections, if this is the case then the stranded neuron is also deleted. Note that a more thorough cleanup routine could be invoked at this point that cleans up any dead-end structures that could not possibly be functional, but this can become complex and so we leave NEAT to eliminate such structures naturally.
Neuron deletion is slightly more complex. The deletion algorithm attempts to replace neurons with connections to maintain any circuits a neuron may have participated in, in further generations those connections themselves will be open to deletion. This approach provides NEAT with the ability to delete whole structures, not just connections.
Because we replace connected neurons with connections we must be careful which neurons we delete. Any neuron with only incoming or only outgoing connections is at a dead-end of a circuit and can therefore be safely deleted with all of it's connections. However, a neuron with multiple incoming and multiple outgoing connections will require a large number of connections to substitute for the loss of the neuron - we must fully connect all of the original neuron's source neurons with its target neurons, this could be done but may actually be detrimental since the functionality represented by the neuron is now distributed over a number of connections, and this cannot easily be reversed. Because of this, such neurons are omitted from the process of selecting neurons for deletion.
Neurons with only one incoming or one outgoing connection can be replaced with however many connections were on the other side of the neuron, therefore these are candidates for deletion.
To test the phased search technique an OCR experiment was devised. OCR is perhaps a misleading term for the experiment since OCR covers a wide range of problems and is most often taken to be the reading of written or printed text. The experiment used here is actually better described as a pattern classification problem, hence the term 'Simple'-OCR. There are 26 patterns, each representing one of the 26 lower case letters of the alphabet. Each pattern is is a bitmap (1 bit-plane image) of size 7 pixels wide by 9 high. There are therefore 7*9=63 pixels in each image, each of which is associated with its own input neuron. An output neuron is defined for each character (so 26 outputs in total) and the task for the evolved networks is to set the output high that corresponds to the character image being applied to the input nodes.
Note then that the 26 character images are fixed with no variation in character size, style, etc. This means that recognition can actually be made on the basis of individual pixels. e.g. if a given character is the only one to have a specific pixel set to 1, then that pixel's input node can be connected directly to the appropriate output to correctly identify the character.
In fact it turns out that the task can be solved without any hidden nodes, and essentially then this is a test of NEAT's ability to search through a high input-output connection search space, although hidden nodes may be beneficial and have not been disabled for the experiment.
| Type Of Run | Parameters | Value |
| All | Population Size | 150 |
| Experiment Duration | 1hr 30mins | |
| Elitism Proportion | 0.2 | |
| Selection Proportion | 0.2 | |
| Min. Species Threshold | 6 | |
| Max Species Threshold | 10 | |
| Species Drop-off Age | 200 | |
| Asexual Offspring Proportion | 0.5 | |
| Crossover Offspring Proportion | 0.5 | |
| Interspecies Mating Proportion | 0.1 | |
| Compatibility Threshold (Initial Value) | 8 | |
| Compatibility Disjoint Coefficient | 1 | |
| Compatibility Excess Coefficient | 1 | |
| Compatibility Weight Delta Coefficient | 1 | |
| Complexifying | Weight Mutation Rate | 0.0979 |
| Add Neuron Rate | 0.001 | |
| Add Connection Rate | 0.02 | |
| Delete Neuron Rate | 0.0 | |
| Delete Connection Rate | 0.0 | |
| Blended | Weight Mutation Rate | 0.958 |
| Add Neuron Rate | 0.001 | |
| Add Connection Rate | 0.02 | |
| Delete Neuron Rate | 0.001 | |
| Delete Connection Rate | 0.02 | |
| Phased | Weight Mutation Rate | 0.0979 |
| Add Neuron Rate | 0.001 | |
| Add Connection Rate | 0.02 | |
| Delete Neuron Rate | 0.0 | |
| Delete Connection Rate | 0.0 |
- Note that during a pruning phase additive mutations are disabled and subtractive mutation rates are controlled by the pruning algorithm.
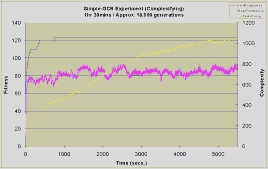
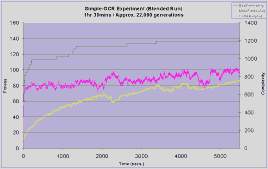
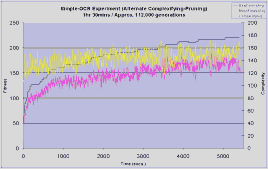
Each experiment was run for 1hour and 30 minutes, instead of for a fixed number of generations. This is necessary because the number of generations achieved in a given duration by the different types of experiment varies considerably. Phased runs typically achieved 112,000 generations whilst the complexifying and blended runs achieved about 18,000 and 22,000 generations respectively.
Each correct output resulted in a fitness of 10 being awarded. Therefore the maximum fitness for all experiments is 26*10=260.
The results shown here are the average of three runs of each type of experiment. There are six graphs in total, one for each type of experiment and a further three showing a comparison of various statistics across the three types of experiment. Click on the small graphs below to see a full screen version. These are optimized PNG images, if you have trouble viewing them please let me know..
With 26*63=1638 possible connections between the inputs and outputs the search space is considerable, and this is reflected in the task's difficulty. The complexification and blended experiments were only able to correctly identify approximately 13 out of the 26 patterns at best, both of these experiments see complexity rise steadily throughout the duration. The slow drop in the rate at which complexity rises is due to the slowing down of the experiments - more complex genomes increase the time between generations.
The complexifying experiment makes an early jump in fitness to 120 in less than 500 seconds and then hardly improves at all over the next 5000 seconds. The blended run shows a similar initial sharp rise, but there is now a gradual improvement over the duration of the search approaching a fitness of 140, which is slightly better then the complexifying run.
The phased experiment performs much better then the other two, with an initial jump in fitness similar to the other two runs but followed by a steady climb in population fitness over the course of the experiment to a high of 220. Also note how the plot of complexity oscillates over a relatively small range (between 30 and 50) as the run switches between pruning and complexifying, but actually oscillates around a constant level throughout the duration of the run, maintaining a much lower level than the complexifying and blended runs.
An interesting side observation during the phased search experiments was that the maximum fitness was often seen to rise slightly during a pruning phase. A possible reason for this is that some connections may have been preventing other connections from contributing to an increased fitness. Traditional NEAT is able to overcome the detrimental effect of such connections by setting their weight at or close to zero. However, this approach may be limited because NEAT must first discover which connections are detrimental by weight mutation, this becomes increasingly difficult as the number of connections rises. On the other hand, when a detrimental connection is finally disabled, this weight may then propagate through the population through reproduction, but this will only happen in significant amounts if the setting of the weight to zero has an immediate benefit, thus causing the genome's fitness to rise. A large proportion of the time this may not be the case, a detrimental connection's removal may make way for beneficial connections, but does not have an immediate beneficial result. Without the immediate feedback of a rise in fitness there is a good chance that the detrimental connection weight will be set back to a non-zero value within a small number of generations, thus exposing only a short window of opportunity for beneficial connections to take advantage of the disabled detrimental connection.
* This is perhaps over simplistic since, e.g. a chain of connections and neurons might be describing the functionality equivalent to a single connection. All this means though is that we can extend the idea by using other, more complex means to identify further types of redundancy.
** The mean population complexity (MPC) is measured as the total number of both neuron and connection genes in the population divided by the population size.
1. Derek James, Philip Tucker : A Comparative Analysis of Simplification and Complexification in the Evolution of Neural Network Topologies. Late breaking paper at GECCO 2004.
Colin,
August, 2004
 Copyright 2004, 2016 Colin Green.
Copyright 2004, 2016 Colin Green.